- a) The number of factors of N is given by the expression (p + 1) (q + 1) (r + 1) ...
- b) It can be expressed as the product of two factors in 1/2 {(p + 1) (q + 1) (r + 1).....} ways
- c) If N is a perfect square, it can be expressed
- (i) as a product of two DIFFERENT factors in 1⁄2 {(p + 1) (q + 1) (r + 1) ... -1 } ways
- (ii)as a product of two factors in 1⁄2 {(p + 1) (q + 1) (r + 1) ... +1} ways
- d) sum of all factors of N =
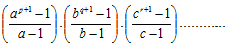
- e) the number of co-primes of N (< N), Φ(N) =
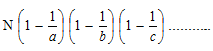
- f) sum of the numbers in (e) = N⁄2.ΦN
- g) it can be expressed as a product of two factors in 2n–1, where ‘n’ is the number of different prime factors of the given number N
I = Interest, P is Principle, A = Amount, n = number of years, r is rate of interest
1. Interest under
2. Amount under
3. Effective rate of interest when compounding is done k times a year re = 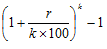
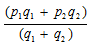
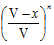
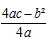 , at x=-b⁄2a
, at x=-b⁄2a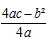 , at x=-b⁄2a
, at x=-b⁄2a| Figure | Perimeter | Area | Diagram |
|---|---|---|---|
| Triangle | a+b+c | √s(s-a)(s-b)(s-c) (or) 1⁄2bh |
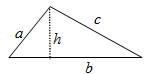 |
| Right Angled Triangle | a+b+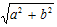 |
½ab | 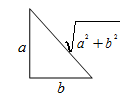 |
| Equilateral Triangle | 3a | √¾ a2 | 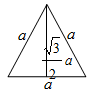 |
| Isosceles Triangle | 2a+b | 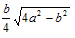 |
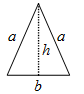 |
| Circle | 2πr | πr2 |  |
| Sector of a Circle | θ⁄360×2πr+2r |
θ⁄360×πr2 | 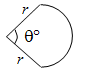 |
| Square | 4a | a2 |  |
| Rectangle | 2(l+b) | l×b |  |
| Trapezium | a+b+c+d | ½(a+b)h | 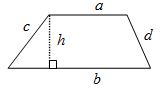 |
| Parallelogram | 2(a+b) | bh or absinθ | 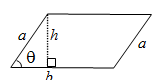 |
| Figure | Lateral Surface Area | Total Surface Area | Volume | Diagram |
|---|---|---|---|---|
| Cube | 4a2 | 6a2 | a3 | 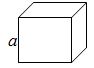 |
| Cuboid | 2h(l + b) | 2(lb + bh + lh) | lbh | 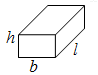 |
| Cylinder | 2πrh | 2πr(r+h) | πr2h | 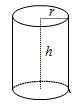 |
| Cone | πrl | πr(l+r) | ⅓πr2h | 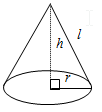 |
| Sphere | - | 4πr2 | 4⁄3πr3 | 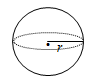 |
| Hemisphere | 2πr2 | 3πr2 | 2⁄3πr3 | 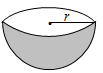 |
| Equilateral Triangular Prism | 3ah | 3ah+ √3⁄2 a 2 | √3⁄4 a 2h | 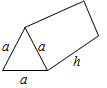 |
| Square prism | 4ah | 2a(2h+a) | a2h | 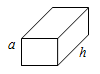 |
| Hexagonal Prism | 6ah | 3a(√3⁄2 a+2h | ½×3 √3 a2 h | 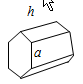 |
| Frustum of a cone | πl(R + r)where,l=√(R-r)2+h2 | π(R2 + r2 + Rl + rl) | ⅓πh(R2+Rr+r2) | 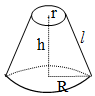 |
| Frustum of a Pyramid | ½× perimeter of base × Slant Height | L.S.A + A1 + A2 | ½× h(A1+A2+√A1A2) |  |
| Torus | - | 4π2ra | 2π2r2a | 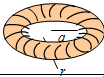 |
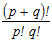
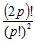 , when the two groups have distinct identity and
, when the two groups have distinct identity and 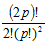 , when the two groups do not have distinct identity
, when the two groups do not have distinct identity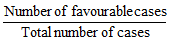 and 0 ≤ P(Event) ≤ 1
and 0 ≤ P(Event) ≤ 1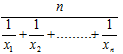
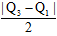 (i.e., one-half the range of quartiles)
(i.e., one-half the range of quartiles)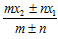 and y =
and y = 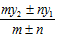 , positive sign for internal division and negative sign for external division
, positive sign for internal division and negative sign for external division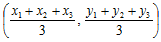
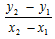
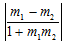
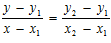
 or m1= m2 (ii) perpendicular if a1 a2 + b1 b2 = 0 or m1m2 =−1
or m1= m2 (ii) perpendicular if a1 a2 + b1 b2 = 0 or m1m2 =−1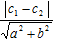
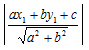
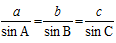 = 2R, where R is the circumradius of triangle ABC
= 2R, where R is the circumradius of triangle ABC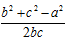 , similarly cosB and cosC can be defined
, similarly cosB and cosC can be defined

 Login
Login

